|
Abstract. An m-partition of Rn is, by definition, a
system of m + n vectors
U = {u1,0, u1,1, u2,0, u2,1, …, um,0, um,1, um+1, …, un} 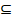 Rn, Rn,
such
that, for every x 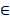 Rn there exists a unique
vector λ sastisfying Rn there exists a unique
vector λ sastisfying
λ = (λ1,0, λ1,1,
…, λm,0,
λm,1,
λm+1,
…, λn)T 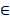 Rm+n, Rm+n,
λi,s 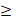 0,
(i, s) 0,
(i, s) 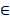 I I
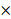 S, S,
λi,0.λi,1 = 0, i 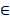 I, I,
x = 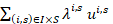 + + 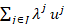 , ,
where I :=
{1, 2, …, m}, J := {m + 1, …, n} and S := {0, 1}.
Systems of this type are
usually encountered in linear complementarity problems. By studying them we
expect to provide some strong tools for investigating theory of
complementarity problems. Specifically, in this paper we shall prove a
basic characterization of partition systems in Rn
and then derive some direct applications to linear complementarity
problems.
|