|
Abstract. Let G be afinite group and nX a conjugacy class of elements of
order n in G. G is called nX−complementary generated if,
for every x 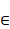 G -
1, there is a y G -
1, there is a y 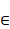 nX
suchthat G =<x,y>. nX
suchthat G =<x,y>.
In [20] the
question of finding all positive integers n such that a given non-abelian finite simple group G is nX-complementary generated was posed. In this paper we answer
this question for the sporadic group Ru.
In fact, we prove that for any element order n of the sporadic group Ru,
Ru is nX-complementary generated if and only if n ≥ 3.
|