|
Abstract. We study closed submanifolds M of dimension 2n + 1, immersed into a (4n
+ 1) -dimensional Sasakian space form (N,
ξ, η,  )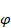
with constant φ-sectional
curvature c, such that the reeb
vector field ξ is tangent to
M. Under the assumption that M has equal Wirtinger angles and
parallel mean curvature vector fields, we prove that for any positive
integer n, M is either an invariant or an anti-invariant submanifold of N if c > -3, and the common Wirtinger angle must be constant if c = -3. Moreover, without assuming
it being closed, we show that such a conclusion also holds for a slant
submanifold M (Wirtinger angles
are constant along M) in the
first case, which is very different from cases in Kähler geometry.
|
