|
Abstract. For a
non-abelian finite group G = <a1, a2, …,an>
the Fibonacci length of G with
respect to the ordered generating set A
= {a1, a2, …, an} is the least integer
l such that for the sequence of elements xi = ai,
1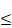 i i
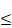 n,
xn+I = n,
xn+I = 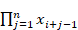 ,
I ,
I 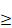 1, of G,
the equations xl+i = ai, 1 1, of G,
the equations xl+i = ai, 1 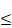 i i
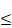 n
hold. The question posed in 2003 by P.P. Campbell that "Is there any
relationship between the lengths of finite groups G, H and G x H?" In this paper we answer this question when at least
one of the groups is a non-abelian 2-generated group. n
hold. The question posed in 2003 by P.P. Campbell that "Is there any
relationship between the lengths of finite groups G, H and G x H?" In this paper we answer this question when at least
one of the groups is a non-abelian 2-generated group.
|