|
Abstract. Let A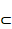 R2
be a nonempty closed convex subset and C R2
be a nonempty closed convex subset and C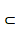 R2
be a nonempty nontrivial convex cone. Due to Luc (1985 and 1989), if A is compact and if the closure R2
be a nonempty nontrivial convex cone. Due to Luc (1985 and 1989), if A is compact and if the closure 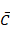 is pointed, then the efficient set E(A|C) of A w.r.t. C is homeomorphic to a nonempty closed interval of R1, whose proof was
completed by Huy, Phuong, and Yen (2002). Huy (2003) extended this result
by replacing the compactness of A
with the compactness of A is pointed, then the efficient set E(A|C) of A w.r.t. C is homeomorphic to a nonempty closed interval of R1, whose proof was
completed by Huy, Phuong, and Yen (2002). Huy (2003) extended this result
by replacing the compactness of A
with the compactness of A 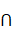 ({a}- ({a}-
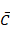 ),
for all a ),
for all a 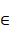 A.
In this paper, we show the same conclusion in a much shorter way and under
essentially weaker assumption, namely C
is pointed and there exists an a A.
In this paper, we show the same conclusion in a much shorter way and under
essentially weaker assumption, namely C
is pointed and there exists an a 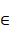 A
such that A A
such that A 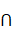 ({a}
- C) is bounded. Moreover, the
weakly efficient set Ew(A|C) w.r.t. any convex cone C
having nonempty interior is homeomorphic to a closed interval in R1 even if C is not pointed. ({a}
- C) is bounded. Moreover, the
weakly efficient set Ew(A|C) w.r.t. any convex cone C
having nonempty interior is homeomorphic to a closed interval in R1 even if C is not pointed.
|