Home
Recent Issues
Volume 53	1
Volume 52	1	2	3	4
Volume 51	1	2	3	4
Volume 50	1	2	3	4
Volume 49	1	2	3	4
Past Issues
The Journal
Cover
Aims and Scope
Subscription Information
Editorial Board
Instructions for Author
Contact Us

Vietnam Journal of Mathematics 34:1(2006) 17-30

Closed Weak Supplemented Modules 

Qingyi Zeng

Abstract.  A module M is called closed weak supplemented if for any closed submodule N of M, there is a submodule K of M such that M = K + N and K 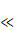N M. Any direct summand of a closed weak supplemented module is also closed weak supplemented. Any finite direct sum of local distributive closed weak supplemented modules is also closed weak supplemented. Any nonsingular homomorphic image of a closed weak supplemented module is closed weak supplemented. R is a closed weak supplemented ring if and only if M_n(R) is also a closed weak supplemented ring for any positive integer n.

Established by Vietnam Academy of Science and Technology & Vietnam Mathematical Society

Published by Springer since January 2013