|
|
|
Vietnam Journal of Mathematics 34:3(2006)
285-294
|
|
Solution to an Open Problem on the Integral
Sum Graphs
|
|
Shuchao Li, Huiling
Zhou, and Yanqin Feng
|
|
Abstract. The concept of the (integral) sum
graphs was first introduced by Harary (Congr. Number 72 (1990) 101;
Discrete Math. 124 (1994) 99). Let N*
denote the set of positive integers. The (integral) sum graph G+(S) of a finite subset S
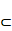 N*(Z) is the graph (S, E) with uv N*(Z) is the graph (S, E) with uv 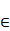 S
if and only if u + v S
if and only if u + v 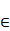 S.
A graph G is called an (integral)
sum graph if it is isomorphic to the (integral) sum graph G+(S) for some S S.
A graph G is called an (integral)
sum graph if it is isomorphic to the (integral) sum graph G+(S) for some S 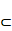 N*(Z). In this paper we give a
constructive method to show that the odd cycles are regular integral sum
graphs, which extends the classes of integral sum graphs and completely
solves an open problem posed by Baogen Xu (Discrete Math. 194 (1999)
285-294). N*(Z). In this paper we give a
constructive method to show that the odd cycles are regular integral sum
graphs, which extends the classes of integral sum graphs and completely
solves an open problem posed by Baogen Xu (Discrete Math. 194 (1999)
285-294).
|
|
|
|
2000 Mathematics Subject Classification: 05C38, 05C78.
|
|
Keywords: Odd cycle, integral sum graph.
|
|
|
|
Established
by Vietnam Academy of Science and Technology & Vietnam Mathematical
Society
Published
by Springer since January 2013
|
|