|
|
|
Vietnam Journal of Mathematics 34:4(2006)
397-409
|
|
Note on Maximal Nonhamiltonian
Burkard--Hammer Graphs
|
|
Ngo Dac Tan
|
|
Abstract. A graph G = (V, E) is called a split graph if there
exists a partition V = I  K
such that the subgraphs G[I] and G[K] of G induced by I and K are empty and
complete graphs, respectively. In 1980, Burkard and Hammer gave a necessary
condition for a split graph G
with |I| < |K| to be hamiltonian. We will call a
split graph G with |I| < |K| satisfying this condition a Burkard - Hammer graph. Further,
a split graph G is called a
maximal nonhamiltonian split graph if G
is nonhamiltonian but G + uv is Hamiltonian for every uv K
such that the subgraphs G[I] and G[K] of G induced by I and K are empty and
complete graphs, respectively. In 1980, Burkard and Hammer gave a necessary
condition for a split graph G
with |I| < |K| to be hamiltonian. We will call a
split graph G with |I| < |K| satisfying this condition a Burkard - Hammer graph. Further,
a split graph G is called a
maximal nonhamiltonian split graph if G
is nonhamiltonian but G + uv is Hamiltonian for every uv 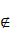 E
where u ∈ I and v ∈ K.
In a nearlier work, the author and Iamjaroen have asked whether every
maximal nonhamiltonian Burkard – Hammer graph G with the minimum degree
δ(G) ≥ |I| - k where k
≥ 3 possesses a vertex with exactly k - 1 neighbors in I.
The first question and the second one have been proved earlier to have a
positive answer for k = 3 and k = 4, respectively. In this paper,
we give a negative answer both to the first question for all k E
where u ∈ I and v ∈ K.
In a nearlier work, the author and Iamjaroen have asked whether every
maximal nonhamiltonian Burkard – Hammer graph G with the minimum degree
δ(G) ≥ |I| - k where k
≥ 3 possesses a vertex with exactly k - 1 neighbors in I.
The first question and the second one have been proved earlier to have a
positive answer for k = 3 and k = 4, respectively. In this paper,
we give a negative answer both to the first question for all k 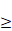 4 and to the second question for all k 4 and to the second question for all k 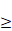 5. 5.
|
|
2000 Mathematics Subject Classification: 05C45.
|
|
Keywords: Split graph, Burkard--Hammer condition,
Burkard--Hammer graph, hamiltonian graph, maximal nonhamiltonian split
graph.
|
|
|
|
Established
by Vietnam Academy of Science and Technology & Vietnam Mathematical
Society
Published
by Springer since January 2013
|
|