|
|
|
Vietnam Journal of Mathematics 35:2(2007)
215-222
|
|
H-Cofinitely Supplemented Modules
|
|
Muhammet Tamer
Kosan
|
|
Abstract. Let M be a right R-module.
We call M H-cofinitely supplemented
if for very cofinite submodule A
of M (i.e. the factor module M/A is finitely generated) there exists a direct summand D of M such that M = A + X holds if and only if M
= D + X. It is shown that in this paper: (1) Let M be an H-cofinitely
supplemented Duo module. Then every direct summand of M is H-cofinitely
supplemented module. (2) Let 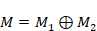 be a Duo module. If M1 and M2
are H-cofinitely supplemented
modules, then M is H-cofinitely supplemented. (3)
Assume Rad(M) << M. Then M is H-cofinitely
supplemented if and only if every cofinite submodule of M/Rad(M) is direct summand and each cofinite direct summand of M/Rad(M) lifts to a direct summand of M. In addition, let M
be a duo right R-module. M is H-cofinitely supplemented if and only if every maximal
submodule of M has an H-supplement in M.
|
|
2000 Mathematics Subject Classification: 16D99.
|
|
Keywords: Duo modules, H-supplemented modules, H-cofinitely
supplemented modules.
|
|
|
|
Established
by Vietnam Academy of Science and Technology & Vietnam Mathematical
Society
Published
by Springer since January 2013
|
|
