|
|
|
Vietnam Journal of Mathematics 35:1(2007)
33-41
|
|
Amenable Locally Compact Foundation
Semigroups
|
|
Ali Ghaffari
|
|
Abstract. Let S be a locally compact Hausdorff topological semigroup, and M(S) be the Banach algebra of all bounded regular Borel measures
on S. Let Ma(S) be
the space of all measures µ 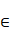 M(S) such that both mapping M(S) such that both mapping 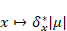 and and 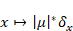 from S
into M(S) are weakly continuous. from S
into M(S) are weakly continuous.
|
|
In this paper, we present a few results in the theory of
amenable foundation semigroups. A number of theorems are established about
left invariant mean of a foundation semigroup. In particular, we establish
theorems which show that Ma(S)* has a left invariant mean. Some
results were previously known for groups.
|
|
2000 Mathematics Subject Classification: 22A20, 43A60.
|
|
Keywords: Banach algebras, locally compact
semigroup, topologically left invariant mean, fixed point.
|
|
|
|
Established
by Vietnam Academy of Science and Technology & Vietnam Mathematical
Society
Published
by Springer since January 2013
|
|