Home
Recent Issues
Volume 53	1
Volume 52	1	2	3	4
Volume 51	1	2	3	4
Volume 50	1	2	3	4
Volume 49	1	2	3	4
Past Issues
The Journal
Cover
Aims and Scope
Subscription Information
Editorial Board
Instructions for Author
Contact Us

Vietnam Journal of Mathematics 36:2(2008) 173-181

 Some Homological Properties of Artinian Modules

Amir Mafi

Abstract. In this paper we show that if (R, m) is a commutative Gorenstein local ring with maximal ideal $\fm$ and $M$ is an Artinian R-module, then depth(R) = Width(M) + sup{i N₀: Ext_Rⁱ(E(R/m), M) 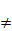0}. Also, we prove that the following statements are equivalent:

(1) R is Gorenstein.

(2) R is Cohen-Macaulay and for any Artinian module M, fd(E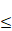(M)) fd(M), where E(M) is an injective envelope of M.

(3) R is Cohen-Macaulay and for any finite length module M of finite injective dimension, id(F(M)) = id(M), where F(M) is a flat cover of M.

2000 Mathematics Subject Classification: 13D01, 13D05, 13D45, 13C11, 13C15, 13H05, 13H10.

Keywords: Artinian modules, Gorenstein injective, Local cohomology modules, Gorenstein rings, Depth.

Established by Vietnam Academy of Science and Technology & Vietnam Mathematical Society

Published by Springer since January 2013