|
where f1,
f2: R - > R, and g1, g2: R2 - > R are continuous
functions, R
= (-∞, +∞), τj(t) 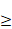 0, j = 1,2, ... m
are bounded continuous functions on R,
and p(t) is a bounded continuous function on R+ = [0,+∞).
We obtain some new sufficient conditions for all solutions and their
derivatives to be bounded, which substantially extend and improve important
results in the literature.
|
