|
Abstract. We say that a regular graph G of order n and degree r  1 (which is not a complete graph) is
strongly regular if there exist non-negative integers τ and θ
such that |Si 1 (which is not a complete graph) is
strongly regular if there exist non-negative integers τ and θ
such that |Si 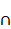 Sj|
= τ for any two adjacent vertices i
and j, and |Si Sj|
= τ for any two adjacent vertices i
and j, and |Si 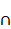 Sj|
= θ for any two distinct non-adjacent vertices i and j, where Sk denotes the
neighborhood of the vertex k. We
here describe the parameters n, r, τ and θ for strongly
regular graphs of order 6(2p+1),
where 2p+1 is a prime number. Sj|
= θ for any two distinct non-adjacent vertices i and j, where Sk denotes the
neighborhood of the vertex k. We
here describe the parameters n, r, τ and θ for strongly
regular graphs of order 6(2p+1),
where 2p+1 is a prime number.
|