|
|
|
Recent
Issues
|
|
Volume 53
|
1
|
2
|
3
|
4
|
|
Volume 52
|
1
|
2
|
3
|
4
|
|
Volume 51
|
1
|
2
|
3
|
4
|
|
Volume 50
|
1
|
2
|
3
|
4
|
|
Volume 49
|
1
|
2
|
3
|
4
|
|
|
Vietnam
Journal of Mathematics 38:4 (2010) 381-393
|
|
On Asymptotic Property of Toeplitz Operators
|
|
Namita Das and
Madhusmita Sahoo
|
|
Abstract.
In this paper we derive certain asymptotic properties of Toeplitz operators
on Hardy and Bergman spaces. More precisely, we have shown that if 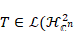 (T))
and (T))
and 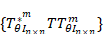 converges to an operator L in the strong operator topology
for all inner functions converges to an operator L in the strong operator topology
for all inner functions 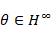 (T)
then (T)
then  , a Toeplitz oper-ator on , a Toeplitz oper-ator on 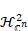 (T)
and if T is an operator in the
Hankel algebra, the norm closed algebra generated by all Toeplitz and all
Hankel operators together on (T)
and if T is an operator in the
Hankel algebra, the norm closed algebra generated by all Toeplitz and all
Hankel operators together on 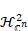 (T),
then the sequence (T),
then the sequence 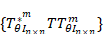 converges to a Toeplitz operator on converges to a Toeplitz operator on 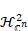 (T)
in the strong operator topology for all inner functions (T)
in the strong operator topology for all inner functions  (T).
As an application, we have shown that if (T).
As an application, we have shown that if 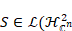 (T))
and (T))
and  is
of fi-nite rank for all is
of fi-nite rank for all 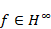 (T)
then (T)
then 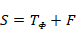 , where , where  (T) (T) and F
is a finite rank operator. This is an extension of the work done for the
scalar valued case in [2] and [12]. Asymptotic properties of Toeplitz
operators and Hankel operators defined on the Berg-man space were also
analysed. and F
is a finite rank operator. This is an extension of the work done for the
scalar valued case in [2] and [12]. Asymptotic properties of Toeplitz
operators and Hankel operators defined on the Berg-man space were also
analysed.
|
|
2000 Mathematics Subject Classification: 47B35.
|
|
Keywords: Hardy space, Bergman space, Toeplitz
operators, Hankel operators, Inner functions.
|
|
|
|
Established
by Vietnam Academy of Science and Technology & Vietnam Mathematical
Society
Published
by Springer since January 2013
|
|