|
Abstract. This paper studies the solvability
of the following higher-order nonlinear neutral delay difference equation
$$ \aligned
\Delta\Big(a_{kn}\cdots\Delta\big(a_{2n}\Delta(a_{1n}\Delta(x_n+b_nx_{n-d}))\big)\Big)
+\sum_{j=1}^sp_{jn}f_j(x_{n-r_{jn}})=q_n, \quad n\ge n_0, \endaligned $$
where $n_0\ge0,n\ge0,d>0,k>0,j>0,s>0$ are integers,
$\{a_{in}\}_{n\ge n_0}(i=1,2,\cdots,k)$, $\{b_n\}_{n\ge n_0}$,
$\{p_{jn}\}_{n\ge n_0}(j=1,2,\cdots,s)$ and $\{q_n\}_{n\ge n_0}$ are real
sequences,  ,
fj ,
fj 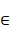 C(R,R) and xfj(x) C(R,R) and xfj(x) 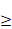 0 for any x 0 for any x 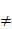 0 (j
= 1,2,…, s). Some sufficient
conditions for existence of nonoscillatory solutions of this equation are
established and expatiated through five theorems according as the range of
value of the sequence bn. 0 (j
= 1,2,…, s). Some sufficient
conditions for existence of nonoscillatory solutions of this equation are
established and expatiated through five theorems according as the range of
value of the sequence bn.
|